Boris Hennig

Next: (1)Up: Wieviele Substanzen gibt es? Previous: Relative Substanzen

Geometrie und Naturwissenschaft

Es ist dann sinnvoll, zu fragen, wozu die Rede von der einen materiellen Substanz gerade im Kontext der wissenschaftlichen Redeweise dient. Offenbar will Descartes von der traditionellen Gepflogenheit Abstand nehmen, einzelne Dinge Substanzen zu nennen. Aristoteles hatte in den Kategorien geschrieben:

Substanz aber ist die hauptsächlich und an erster Stelle und vorzüglich genannte, die weder von einem zu Grunde Liegenden ausgesagt wird noch in einem zu Grunde Liegenden ist, zum Beispiel der individuelle Mensch oder das individuelle Pferd.

Grob gesagt ist hier dasjenige eine Substanz, das in einem Satz nicht von anderem ausgesagt wird. In dem Satz ,Ein Pferd ist teuer` wird nicht das Pferdsein ausgesagt, sondern das Teuersein. Substanzen werden nicht ausgesagt oder zugeschrieben, sondern durch Subjektworte (nomina) bezeichnet.Entsprechend hatte auch die Logik noch nicht konsequent mit Variablen gearbeitet. Die Rede über Dinge hatte es zunächst mit Namen oder natural kind terms zu tun und nicht mit unbestimmten Substanzen und deren Eigenschaften. Die mittelalterliche, aristotelisch geprägte Logik hatte, grob skizziert, Subjektworte (nomina) von Prädikatworten unterschieden. Subjektworte bezeichnen Substanzen, mit den Prädikatworten wird einer so bezeichneten Substanz eine Eigenschaft zugesprochen. Die scholastische Urteilstheorie ist freilich um einiges komplizierter, so dass einer der Vorzüge der zu Descartes' Zeit beginnenden modernen Logik eher deren Einfachheit ist.

Petrus Hispanus, Verfasser eines einflussreichen Logik-Lehrbuchs aus dem 13. Jahrhundert, unterscheidet verschiedene Ebenen, auf denen die Zuschreibung einer Eigenschaft geschieht. Erstens bezeichnet jedes Nomen ein Ding mittels einer Eigenschaft.

Zweitens kann dem, was das Nomen so herausgreift, eine weitere Eigenschaft durch einen Behauptungssatz zugesprochen werden. In dem Satz ,Alle Menschen sind sterblich` wird durch das Nomen ,Mensch` eine Substanz anhand einer gewissen Eigenschaft, ,Menschlichkeit` etwa, bezeichnet. Eine weitere Eigenschaft, sterblich zu sein, wird dann der menschlichen Substanz zugesprochen. Die Naturphilosophie hatte dementsprechend Aussagen über Gold, Steine oder sublunare Materie machen können, in der folgenden Form:

Jedes F ist ein G.

Dagegen weist Descartes darauf hin, dass die Wissenschaft von der körperlichen Substanz, die er im Auge hat, nicht von einzelnen Dingen handelt, sondern stets von der ganzen ausgedehnten Welt.Ein Vorspiel hat dies im Streit um die Substanz des Brotes beim Abendmahl. Laut christlicher Lehrmeinung verwandelt sich das Brot, das beim Abendmahl gereicht wird, in den Körper von Jesus Christus.

Dies im Rahmen einer Physik zu erklären, war stets ein notorisches Problem.

Thomas von Aquin hatte geschrieben, das Brot verliere durch das Wort des Priesters

seine Brot-Substanz und bestehe fortan als Corpus Christi weiter, indem lediglich sein Ausgedehntsein erhalten bleibe.

Interessant ist an dieser Theorie vor allem, dass der Unterschied zwischen Brot und Corpus Christi nur durch eines festgestellt werden kann: Man achtet darauf, was der Priester sagt. Dessen Worte werden dadurch zu einem performativen Sprechakt und der Unterschied der Substanzen zu einem gesellschaftlichen, weil lediglich anhand einer Kommunikation identifizierbaren, Tatbestand.

Descartes spricht entsprechend vom ,,Wunder der Substanzumwandlung, das nur durch die Worte des Priesters erschließbar ist.``

Arnauld hatte in seinen Einwänden auf die Meditationen beklagt, Descartes mache die Substanzlosigkeit des Brotes beim Abendmahl zum Normalfall.

Dieser erwiderte, gerade dadurch mache seine Physik die Substanzumwandlung fassbar.

Descartes kann dies allerdings nur behaupten, weil seine Physik von vornherein nichts als die Ausdehnungseigenschaften berücksichtigt. Daher ist seine Substanzlehre mit der thomistischen Theorie über das Abendmahl kompatibel: Zwar hat der Sprechakt des Priesters weiterhin seine religiöse Funktion, physikalisch aber ändert er nichts am Brot, da dieses seine Ausdehnungseigenschaften beibehält. Descartes gesteht hiermit insbesondere gegenüber der Theologie ein, dass seine Physik zwar stringent und korrekt die Welt der ausgedehnten Körper beschreibe, aber nicht vollständig, indem sie nämlich nicht zwischen Brot und Corpus Christi zu unterscheiden vermag. In diesem Punkt wird ihm Arnauld, in seiner epochemachenden Logik von Port Royal, schließlich folgen.

Dort wird er auch beklagen, dass Eigenschaften bisher mit echten Substanzen vermischt worden seien.

Es ist höchst wichtig, zu wissen, was wirklich ein modus ist und was nur so scheint, weil es eine der Hauptursachen unserer Fehler ist, die modi mit den Substanzen zu vermischen.

Auf der einen Seite streben Descartes und Arnauld danach, Substanzzuschreibungen und Eigenschaftszuschreibungen voneinander zu trennen. Sie erkennen nur zwei Arten von Substanzen an, entsprechend den zwei Klassen klarer und deutlicher Begrifflichkeit, aber viele Eigenschaften. Damit verläuft die Unterscheidung zwischen Substanz und Eigenschaft parallel zu der zwischen Attribut und modus. Es ist Eines, einem Ding verschiedene modi zuzuschreiben, und ein Anderes, den Bereich der Eigenschaften, also die Substanz, von der die Rede ist, zu wechseln. Andererseits vereinheitlicht Descartes damit gerade den Bereich der Subjekte, von denen die Rede sein kann. Das Wort Dreieck bezeichnet für ihn nicht mehr eine dreieckige Substanz, sondern eine ausgedehnte Substanz in dreieckiger Form. Dreieckigkeit ist kein unveränderliches Attribut. Damit bezeichnen zwei verschiedene Subjektworte im Bereich des ausgedehnten, etwa Dreieck und Quadrat, dieselbe Substanz in verschiedenen Teilen und Formen. Indem substantielle Eigenschaften wie die der Ausdehnung für einen ganzen Bereich von Sätzen, wie den der Sätze der Geometrie, einheitlich vorausgesetzt werden, unterscheidet Descartes streng zwei Verfahren: (a) die Angabe einer Eigenschaft eines Dinges, (b) der Wechsel des Redebereiches aller Dinge, von denen gehandelt wird. In diesem Sinne fordert Descartes, seine beiden Substanzen streng voneinander zu unterscheiden. Wer von der Rede über Ausgedehntes zu der Rede über Denkendes übergeht, muss sich darüber im klaren sein, dass er den Redebereich vollständig wechselt.Dies hat auch zur Folge, dass Descartes innerhalb der Physik vollständig auf die Benennung von Substanzen verzichten kann.

Denn Substanzen müssen nur namhaft gemacht werden, wenn es gilt, den Redebereich zu wechseln. Der Redebereich der Physik fällt für Descartes mit dem der Geometrie zusammen.

Nicht nur eignet sich die Geometrie dazu, physikalische Objekte zu beschreiben, die physikalische Welt ist geradezu mathematisch. Ernst Cassirer schreibt in seinem Buch über Descartes:

Die Frage, wie eine ,,Anwendung`` der Mathematik auf die Natur möglich ist, hat Descartes nicht gestellt. Er brauchte sie nicht zu stellen: denn er erkannte zwischen den beiden Gebieten keinen Trennungsstrich (...) an.

Auch erkannte Descartes keinen Unterschied zwischen Geometrie und Mechanik an, da er in der Physik grundsätzlich die Annahme von Kräften wie der Schwerkraft verweigerte.

Die Mechanik und mehr noch die Newtonsche Physik stellt nicht in erster Linie dar, wie konkrete einzelne Dinge sich verhalten, sondern wie ,essich` mit der ganzen ausgedehnten Welt verhält. Eine der wichtigsten Neuerungen in der Astronomie der Neuzeit ist, dass man begann, dieselben Gesetze auf irdische Körper wie auf Planeten anzuwenden.

Zuvor hatte man die sogenannte sublunare Materie von den Planeten strikt unterschieden. Der Redebereich ist das, wofür die Sätze gelten, und durch die Vereinheitlichung dieses Bereiches werden mehrere Sätze aufeinander beziehbar, indem sie von Demselben handeln. Die cartesische Physik formuliert Naturgesetze, die für alles Ausgedehnte gelten und die prinzipiell die Form haben: ,,Für alle x gilt, dass die Eigenschaft F mit der Eigenschaft G so und so zusammenhängt.`` Auf einer anderen Ebene muss nun dazu gesagt werden, was alles als x gelten kann. In moderner Prädikatenlogik:

für alle x (Fx impliziert Gx), wobei x aus M

Die cartesische Physik etwa bewegt sich von vornherein im Bereich M beliebiger ausgedehnter Dingen und alle weiteren Terme werden als reine Eigenschaftsworte gewertet. Der obige Satz spricht nicht mehr über eine F-Substanz, der eine G-Eigenschaft zukommt, sondern über das Verhältnis zwischen zwei Eigenschaften F und G einer M-Substanz. Das bedeutet auch, dass Eigennamen in der Physik nicht für Einzeldinge stehen sollten, sondern bestenfalls für Zahlen und Konstanten.

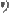Alle Gegenstände der Physik sind als Bündel von Eigenschaften der einen ausgedehnten Substanz, also unter Verzicht auf genuine Namensgebung, beschreibbar.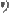

Die moderne Prädikatenlogik hat Descartes nicht zur Verfügung gestanden, Vorbild für seine wissenschaftliche Methode war vielmehr Euklids Geometrie. Die Elemente Euklids waren unter anderem 1533 in Basel erschienen, im Vorwort dieser Edition empfahl Simon Gyrenaeus die Geometrie als absoluta et perfecta formula ohne Rhetorik, als Vorbild aller Künste. Sie beginnen mit einer Reihe von Definitionen, in denen Punkte, Linien und Flächen erklärt werden, und zwar vollständig anhand von Eigenschaften.

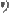Damit ergeben sich insgesamt drei Argumente für die cartesische Trennung zwischen der ausgedehnten Materie und den denkenden Substanzen.

Next: (1)Up: Wieviele Substanzen gibt es? Previous: Relative Substanzen